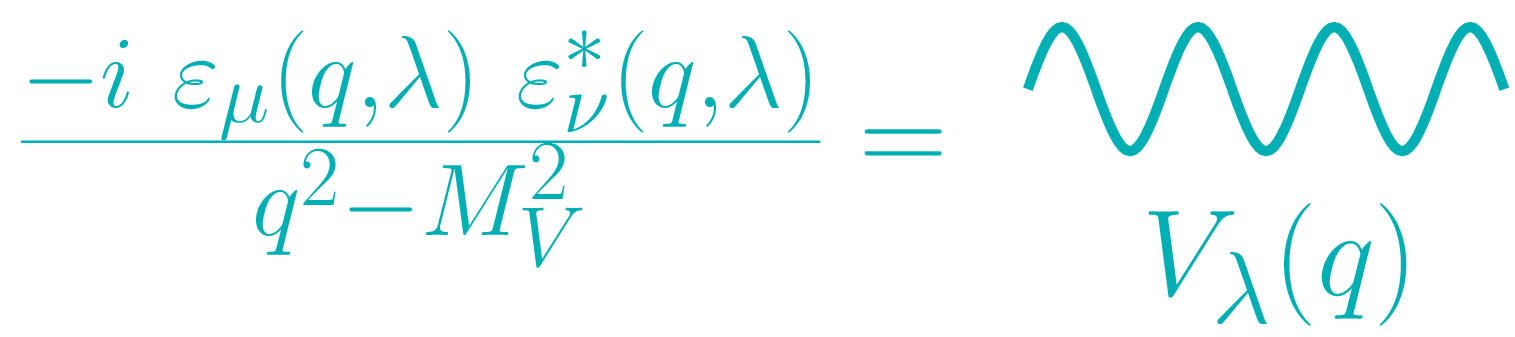wiki:VPolarization

VPolar: The Standard Model at NLO in QCD with helicity-polarized W and Z bosons

Contact Author

Richard Ruiz

  • Institute of Nuclear Physics Polish Academy of Science (IFJ PAN)
  • rruiz AT ifj.edu.pl

In collaboration with:

  1. Javurkova, R.C.L. de Sá, and J. Sandesara ​arXiv:2401.17365 [ 1 ]
  2. Buarque Franzosi, O. Mattelaer, and Sujay Shil ​arXiv:1912.01725 [ 2 ]

Usage resources

  • For instructions and examples on using the VPolar UFO libraries, see M. Javurkova, et al, ​arXiv:2401.17365 [ 1 ]
  • For additional background, see also D. Buarque Franzosi, et al, ​arXiv:1912.01725 [ 2 ]
  • See Validation section below for additional information
  • Special note: this UFO was developed using MG5aMC and calls the 1L, 1T, and 1A propagators defined in ALOHA (see aloha_object.py and create_aloha.py). These may be defined differently in other generators. If they are not defined in your favorite generators, they must be added to the propagators.py file in the VPolar UFO. The file particles.py must then be updated to reflect the propagator names. R. Ruiz is happy to assist with this.

Citation requests

Model Description -- helicity polarization as a Feynman rule

The broad idea of the helicity polarization as a Feynman rule is to treat the helicity-truncated propagator (see [ 2 ] for details) as the Feynman rule for a particle that sits in a definite helicity polarization. The helicity-truncated propagator is given by 

\begin{align}
\Pi_{\mu\nu}^{V\lambda}(q) = \frac{-i\varepsilon_\mu(q,\lambda)\ \varepsilon^*_\nu(q,\lambda)}{q^2-M_V^2 +iM_V\Gamma_V}
\end{align}

and is related to the full propagator by

\begin{align}
    &\Pi_{\mu\nu}^V (q) =
    \frac{-i\left(g_{\mu\nu} - q_\mu q_\nu / M_V^2\right)}{q^2-M_V^2 +iM_V\Gamma_V}\
    \\
    &=\sum_{\lambda\in\{0,\pm1,A\}} 
    \eta_\lambda\ \left(
    \frac{-i\varepsilon_\mu(q,\lambda)\ \varepsilon^*_\nu(q,\lambda)}{q^2-M_V^2 +iM_V\Gamma_V} \right)\ .
\end{align}

Here, $\eta_\lambda=+1$, unless $\lambda=0$ and $V_{\lambda}$ is in the t-channel; in that case $\eta_\lambda=-1$.

By making the graphical identification

mgPolar_FeynmanRule

then one can interpret the full propagator in Eq. 3 as the sum of propagators (or interfering graphs) for a collection of particles $V_\lambda$, where each $V_\lambda$ has its own propagator.

The VPolar UFOs implement this idea for the W and Z bosons.

UFO Description and Usage

ZPolar

  • The SM_Loop_ZPolar UFO contains the SM Lagrangian and includes QCD counter terms up to NLO in QCD. (This means it can be used for both tree-level computations and loop-level computations up to one loop in QCD.) Importantly, the SM Z boson has been replaced with the longitudinal state Z0, the transverse state ZT, the auxiliary state ZA, and the unpolarized state ZX. The state ZX is essentially the original Z boson.

WPolar

VPolar

LO UFOs

Regenerating NLO UFOs

Computing the counter terms (WriteCT[] in NLOCT) is incredibly memory intensive. WPolar and ZPolar each requires 10+ GB of RAM. VPolar requires 20ish GB of RAM. The output of NLOCT for VPolar (2023_0201_SM_Loop_VPolar_FA.nlo) is provided for convenience (see attachments).

Usage in MG5aMC@NLO

For usage in MadGraph5aMC@NLO, see the appendix of M. Javurkova, et al, ​arXiv:2401.17365 [ 1 ].

Studies that have used the above model files

  • Please email to update this space.

References

[1] M. Javurkova, R. Ruiz, R. Coelho Lopes de Sa, and J. Sandesara, Polarized ZZ pairs in gluon fusion and vector boson fusion at the LHC, ​arXiv:2401.17365

[2] D. Buarque Franzosi, O. Mattelaer, R. Ruiz, S. Shil, Automated Predictions from Polarized Matrix Elements, JHEP 2020, 82 (2020) ​arXiv:1912.01725

Last modified 3 months ago Last modified on Sep 24, 2024, 10:17:32 AM

Attachments (14)

Download all attachments as: .zip

Note: See TracWiki for help on using the wiki.