Glance on cosmic strings

Since we are interested in the very early times of the Universe, the temperature and density take such extremal values that matter should only be decribed by particle physics theories, i.e. quantum field theory. A generic prediction of the Standard Model of particle physics, and confirmed in the accelerators, is the unification of two kind of fundamental forces: the electromagnetic and weak ones into what we call the electroweak theory. The spontaneous symmetry breaking mecanism is actually the best candidate for doing this job, and bound to be confirmed by the detection of the Higgs particle. It also gives the energy scale above which the cosmology is called "primordial", i.e. one thousand GeV, or an universe which is a hundredth of a billonth of a second old. In this framework, T. Kibble found, in 1976 [1], that phase transitions induced by spontaneous symmetry breaking mechanisms, similar to the one used in the Standard Model, may generate topological defects. These objects are stable for topological reasons, and although they have not yet been detected, they could be present nowadays ! The compatibility of their existence with the cosmological observations (BOOMERanG, MAXIMA, ARCHEOPS, MAP and PLANCK ...) leads to new constraints on the physics they are stemming from, and thus, at energy scale much higher that the ones reacheable in the accelerators.

The cosmic strings are a lineic kind of topological defect and are currently compatible with the astrophysical constraints. Their existence (or non-existence) can only be confirmed by means of subtle physical effects, and there is a hope that the precise mesurement of the temperature fluctuations of the cosmic microwave background radiation (CMB) give a answer to this question.

This is allowed by means of our theoretical knowledge on these objects. Being extremely massive, and moving with velocities close to the speed of light, the cosmic strings generate gravitationnal perturbations that may be seen in the CMB fluctuations. The angular spectrum of the currently observed fluctuations exhibits severals oscillations with respect to the angular size (see Fig. 1). These oscillations are easily explained in the framework of structure formation models which involve "coherent" perturbations, as it is the case in the famous inflationary model. On the other hand, most of structure formation models involving topological defects cannot predict such oscillations as can be seen on figure 1 where it is represented, in orange, the power spectrum induced by a particular kind of topological defects, "global" say, (somehow irrealist but easier to study). The perturbations are thus called "incoherent", and we expect similar behaviors for the cosmic strings [2,3,4,5]. Nevertheless, the coexistence between inflationary scenario and topological defects seems to be favoured from several point a view. First, the inflationary mecanism itself can give rise to strings [6,7], while the field which drives the inflation, the "inflaton", may end in phase transtions that may also produced topological defects. On the figure 1 is represented the best fit of the actual datas concerning the fluctuations of the CMB by a mix between inflation and the global defects. Although the degeneracy is high, it is interesting to note that the observationnal datas are better ajusted by such a mix [8].

Figure 1: Angular power spectrum for the temperature fluctuations of the CMB predicted by a mix between inflation and " global" defects (a somehow irrealist kind of defect but easier to deal with). The ratio giving the best fit with the datas is also computed (from [8]).

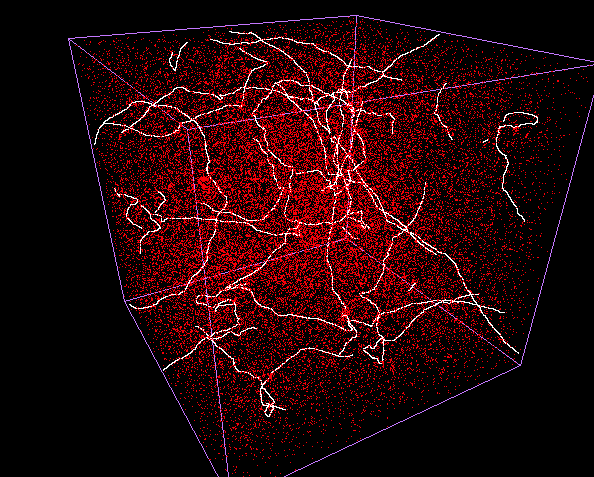
Currently, we are trying to determine precisely the weight of perturbations generated by local cosmic strings in the temperature fluctuations spectrum of the CMB. For doing this, it is first necessary to compute the evolution of a network of cosmic strings during the expansion of the universe. This task is done by integrating the equations of motion of each string in a background chosen to be the Friedmann-Lemaître-Robertson-Walker spacetime, and by considering the "intercommutations" of strings. Indeed, each time two strings (or two different parts of one string) cross, they exchange their respective segment (see Fig. 2).

Figure 2: Loop formation by means of intercommutation of one, or two strings.

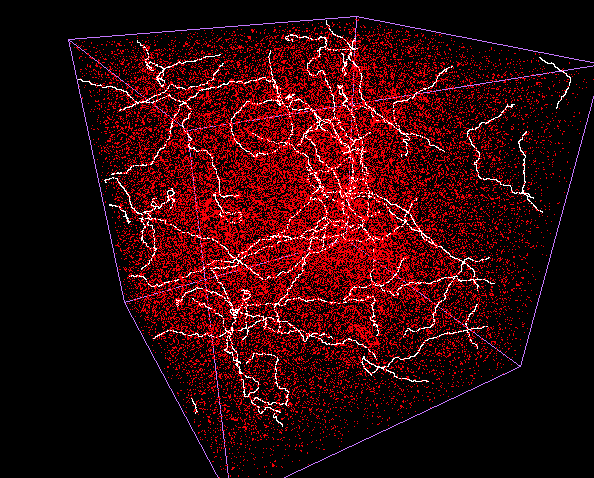
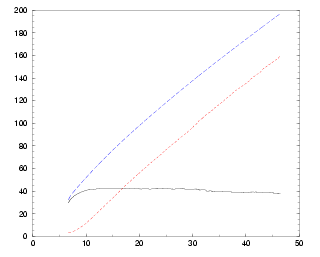
This work has already been performed by F. R. Bouchet and D. Bennett in the 1990 by the development of a numerical code [15,16,17,18,19], and also by another code created by B. Allen and E. P. S. Shellard [13,14]. The main result is that, whatever the initial configuration of the cosmic strings network, this one always relaxes toward a stationnary state in which few "infinite" strings (of length larger than the observable universe) coexist with an incredible quantity of little oscillating loops radiating gravitational waves (see Fig. 3). A first constraint stems from these loops which have to disappear in radiation in order to not overcrowed the universe ! (see Fig. 4). This is usually the case owing to the emission of gravitational waves, but it also may not be the case when particle currents are flowing along the string. In conclusion, it is sufficient to study the cosmic strings statistical properties in this "scaling" regime in order to extrapolate them to cosmological time scales (see Fig. 4).

Figure 3: Cosmic strings network configuration in the matter era (top) and radiation era (bottom) during the "scaling" regime and when the initial comobile volume (the box) enters in the observable universe. The network microstructure clearly appears in the shape of the strings and the size and number of little loops, in red. Most of them are under the picture resolution and appear as points ! (See however the movie below.) C. Ringeval, F. Bouchet

Figure 4: Evolution, with respect to the conformal time in the radiation era, of the rescaled energy density associated with the long strings, in black, compared to the one associated with the little loops, in red, and the total one, in blue. The scaling regime can only take place if the energy associated with the loops dissapears into radiation, which is usually the case by means of gravitational radiation.

Owing to these numerical simulations, it is possible to compute the evolution of all the other cosmological perturbations while taking into account the gravitational influence of the cosmic strings network, this one just acting as an additional source term. Of course, this is only allowed because the cosmological perturbations do not affect the cosmic strings network evolution, whereas the contrary is true. As a result, we can compute separately the evolution of the strings network, and then the evolution of the cosmological perturbations, easier technically.

At the end, the comparison between the computed angular spectrum and the mesured one should constraint the relative ratio between the inflationary perturbations and those generated by the cosmic strings.

Unfortunately, there is a human (more precisely computer) issue, due to the small simulation size currently computable. This problem leads to the abscence of perturbations with characteristic length scale larger than the horizon (the size of the observable universe) "superhorizon" say. Indeed, in order to reach the scaling regime during the numerical simulation, it is necessary to fix an initial strings density not too far from the scaling one (see Fig. 4). Moreover, in order to get superhorizon modes, we have to decrease the initial size of the horizon in our simulation, and if we also want to preserve initial energy density close the the scaling one, it is necessary to increase the total number of strings, and thus the size of the simulation. The superhorizon modes are very important since they determine the behavior of the power spectrum at large angular scale, and thus its normalization with respect to the COBE datas. The solution is to use supercomputers (IAP, UNIGE, IDRIS...), which however require many improvements of the existing codes, but allow now the determination of these superhorizon modes !

The computers used in cosmic strings simulations, allowing the determination of the strings influence in the CMB...(and also the creation of movies !)

1 Go MKV x264 format

The signature detection of cosmic strings in the power spectrum of the CMB depends, from a numerical point of view, on the maximal size of the simulations that can be performed. An answer to the existence or non-existence of cosmic strings in the universe would be a important scientific result, whatever the answer. Indeed, the non-existence of cosmic strings would put constraints on particle physics at very high energy scales (those reached only in the early universe) by prohibiting phase transitions leading to their formation. It is also possible to show that currents can flow along cosmic strings turning them into conducting wires and traps for the particle existing in the primordial universe [9,10,11,12].