Testing the complex mass scheme implementation

The complex mass scheme is the modern way of handling finite width effects of unstable particles in perturbation theory. In a nutshell, it consists in redefining the mass of unstable particles as complex with an imaginary part proportional to its width. The denominator of unstable propagators remains identical, but contrary to the naive implementation of the width, the complex mass will also appear in the numerator of fermion propagators and in all couplings proportional to the unstable particle mass. In doing so, the Lagrangian is simply continued to complex masses and the final result remains gauge invariant. The Complex Mass Scheme (CMS henceforth) can be activated by simply typing the following command in the interactive shell:

MG5_aMC> set complex_mass_scheme True/False

The CMS implementation is rather straightforward at leading-order (LO) but it becomes more involved at next-to-leading-order (NLO) because of mainly two points

• The widths must be LO accurate at least in the offshell region and NLO accurate in the onshell region.
• The logarithms appearing in the UV wavefunction renormalization must be evaluated in the correct Riemann sheet.

The details of these issues will be discussed in a forthcoming publication; This wiki page is mainly to describe the various options to the command 'check cms' which automatically tests the consistency of the CMS implementation. The core idea of the test is to compare amplitudes in the CMS scheme ($\mathcal{A}_{\text{CMS}}$) and in the case of widths set to zero ($\mathcal{A}_{\Gamma=0}$) for a given kinematic configuration where all resonances are far off-shell. The difference between these two amplitudes must be higher order. More formally, this means $\mathcal{A}^{{\text{Born}}_{\text{CMS}}\sim \mathcal{A}}{\text{Born}}_{\Gamma=0} \sim \mathcal{O}(\alpha^a)$.

Then, if we write $(\mathcal{A}^{{\text{Born}}_{\text{CMS}}-\mathcal{A}}{\text{Born}}_{\Gamma=0})/\alpha^{a \equiv \Delta}{\text{LO}} = \kappa^{{\text{LO}}_0 + \kappa}{\text{LO}}_1 \cdot \alpha + \mathcal{O}(\alpha^{2) $, the statement that difference is higher order is equivalent to state that $\kappa}{\text{LO}}_0=0$. At NLO, this relation translates to :

$((\mathcal{A}^{{\text{Virtual}}_{\text{CMS}}+\mathcal{A}}{\text{Born}}_{\text{CMS}})-(\mathcal{A}^{{\text{Virtual}}_{\Gamma=0}+\mathcal{A}}{\text{Born}}_{\Gamma=0}))/\alpha^{{a+1} \equiv \Delta}{\text{NLO}} = \kappa^{{\text{NLO}}_0 + \kappa}{\text{NLO}}_1 \cdot \alpha + \mathcal{O}(\alpha^{2) $}

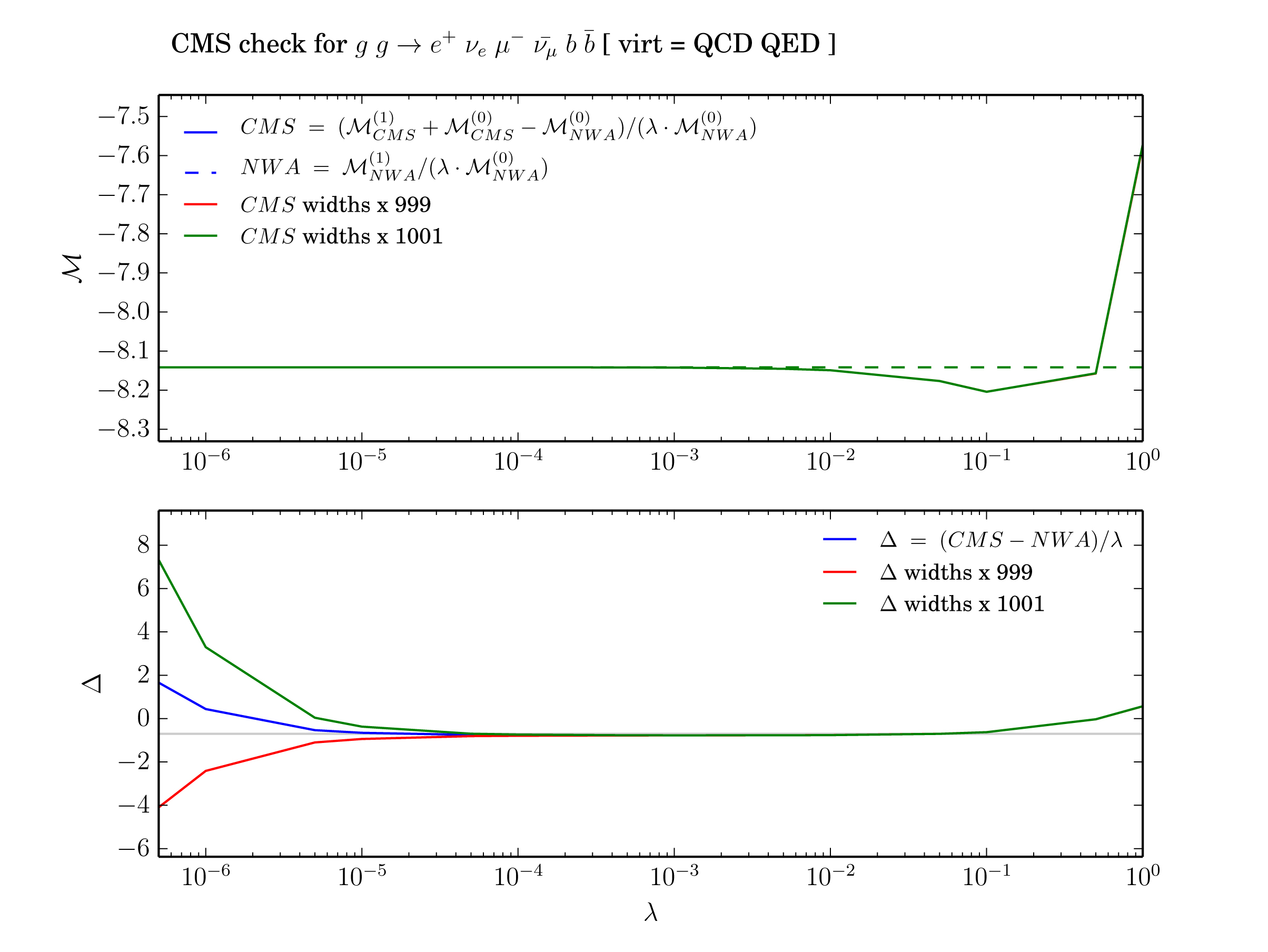
In order to check that $\kappa^{{\text{LO}}_0$ and $\kappa}{\text{NLO}}_0$ are indeed zero, the test proceeds by scaling down all relevant couplings and widths by the parameter $\lambda$ and to evaluate the expressions of $\Delta$ for many progressively smaller values of \lambda but always on the same offshell kinematic configuration. One can then plot the quantities $\Delta^{{\text{NLO|LO}}/\lambda$ and make sure that the asymptot for small values of lambda is the constant $\kappa}{\text{NLO|LO}}_1$. Any divergent behavior would be a manifestation of the presence of the term $\kappa^{{\text{NLO|LO}}_0/\lambda$ which reveals an issue with the CMS implementation (most likely one of the two points mentioned above) which spoils the expected cancellation. Before we detail the option of this test, here is the expected output (generated automatically, incl. this plot) for the case of QCD and QED corrections to fully decayed top quark pair production:}

In the upper inset, we clearly see the finite width effects for large values of $\lambda$. These become progressively smaller and indiscernible below $10^{{-3}$. When dividing this difference by lambda, as done in the lower inset, we only see a mild deviation with respect to a constant. Changing the LO width used for the test by as little as 0.1 % already yields a larger $\kappa}{\text{NLO}}_0$ than the residual one stemming from numerical inaccuracies. The figure on the left shows that incorrectly setting the analytical continuation of UV wavefunctions counterterms logarithms yields an asymptotic value of several thousands in the $\Delta^{{NLO}/\lambda$ plot. This clearly establishes the sensitivity of the test towards any incorrect CMS implementation at NLO.}

We now focus on the description of the command for this check, whose main syntax is

MG5_aMC> check cms [-reuse] <process_definition> <options>

First, the '-reuse' following 'cms' specifies that you want to reuse relevant information existing from previous runs. This includes potentially reusing the fortran output of the NLO matrix element if the same process was run before with the 'cms check' command. Also, if a name was given to this run (see option '--name' further) and the corresponding saved result python pickled file exists on disk, this run will be skipped and the result recycled from the pickle file. When '-reuse' is not specified, the test always restarts from scratch. In general, it is recommended to always use '-reuse'.

The <process_definition> which follows can be any process following the MG5 syntax. If this process is LO, the test will be adapted to test $\kappa^{{\text{LO}}_0$ and the matrix element will be generated an evaluated dynamically directly in python. If the process definition is at NLO, then the test will test $\kappa}{\text{NLO}}_0$ and the output will be done in fortran on disk, compiled and the corresponding standalone 'check' executable steered by MG5_aMC. The LO CMS test is mostly trivial, but it can be useful to investigate the expected sensitivity on the CMS implementation of the corresponding NLO process.

Finally, the following options are available (presented along with their default value)

Basic options

--name=auto

This will serve as the base_name for the fortran output folder for the loop matrix element and for the pickle files storing the results generated. The default 'auto' tries to smartly automatically assign one, but it is recommended to specify your own.

• Example: --name=fully_decayed_ttx

--seed=666

Changes the seed for the generation of the offshell kinematic configuration, allowing for varying the config. The value '-1' sets it so that it is different for every run.

• Example: --seed=667

--offshellness=10.0

Sets what is the minimum requirement of offshellness for each resonance that the kinematic configuration must satisfay. The default offshellness $\chi$ of 10 is such that the momentum of each resonance must satisfy $p^{2>(\chi+1)M$. The offshellness can be negative too, but always strictly larger than -1. Notice that when the offshellness required is negative, it is not guaranteed that MG5_aMC will find a valid kinematic configuration if external states are massive. Finally, notice that the phase kinematic configuration chosen satisfies extra requirement of isolations and hardness in terms of a minimal pt cut and $\delta$R between all external legs.}

• Example: --offshellness=-0.7

--energy=5000.0

Sets the target energy for the kinematic configuration to build. Notice that this energy will be automatically changed with a warning depending on its consistency with the offshellness required.

• Example: --energy=2000.0

Special option

--analyze=None

This option must be used without any process definition. It is intended to specify the path of pickle files storing the results of previous results to be re-analyzed and replotted. A common usage of this option is:

• Example: check cms --analyze=my_default_run.pkl,increased_widths.pkl(Increased_widths),logs_modified.pkl(Inverted_logs),seed_668.pkl(Different_seed)

This will reanalyze the data in my_default_run.pkl and plot them while also including the curves from the list of pickle paths following the first one. The name in parenthesis will serve as the legend (underscores will be replaced by spaces)

More technical options

--cms=QED&QCD,aewm1->10.0/lambdaCMS&as->0.1*lambdaCMS

This is one of the most complicated options and it contains two parts separated by a comma. The first part lists the coupling orders which take part in the expansion. The second part lists how to scale the corresponding parameter which drive the expansion. These must be external parameters present in the param_card. The value 'lambdaCMS' is a special tag which refers to the current value of the scaling parameter $\lambda$ being considered. Notice that these replacement rules must be of the form <ext_param_name>->f(<ext_param_name>,lambdaCMS) where f is some function following python syntax. The default value start from fixed values 10.0 and 0.1 for $\lambda=1$, but it is possible to specify the original value of the parameter in the card like this 'aewm1->aewm1/lambdaCMS' in which case the base value of the external parameter aewm1 will be the one in the original param_card.dat. You should not need to change this default unless you are testing a new physics model with an extended gauge sector (in which case the modification could look like the example below).

• Example: --cms=QED&QCD&NP,aewm1->10.0/lambdaCMS&as->0.1*lambdaCMS&newExpansionParameter->newExpansionParameter*lambdaCMS