Testing the complex mass scheme implementation

The complex mass scheme is the modern way of handling finite width effects of unstable particles in perturbation theory. In a nutshell, it consists in redefining the mass of unstable particles as complex with an imaginary part proportional to its width. The denominator of unstable propagators remains identical, but contrary to the naive implementation of the width, the complex mass will also appear in the numerator of fermion propagators and in all couplings proportional to the unstable particle mass. In doing so, the Lagrangian is simply continued to complex masses and the final result remains gauge invariant. The Complex Mass Scheme (CMS henceforth) can be activated by simply typing the following command in the interactive shell:

MG5_aMC> set complex_mass_scheme True/False

The CMS implementation is rather straightforward at leading-order (LO) but it becomes more involved at next-to-leading-order (NLO) because of mainly two points

• The widths must be LO accurate at least in the offshell region and NLO accurate in the onshell region.
• The logarithms appearing in the UV wavefunction renormalization must be evaluated in the correct Riemann sheet.

The details of these issues will be discussed in a forthcoming publication; This wiki page is mainly to describe the various options to the command 'check cms' which automatically tests the consistency of the CMS implementation. The core idea of the test is to compare amplitudes in the CMS scheme ($\mathcal{A}_{\text{CMS}}$) and in the case of widths set to zero ($\mathcal{A}_{\Gamma=0}$) for a given kinematic configuration where all resonances are far off-shell. The difference between these two amplitudes must be higher order. More formally, this means $\mathcal{A}^{{\text{Born}}_{\text{CMS}}\sim \mathcal{A}}{\text{Born}}_{\Gamma=0} \sim \mathcal{O}(\alpha^a)$.

Then, if we write $(\mathcal{A}^{{\text{Born}}_{\text{CMS}}-\mathcal{A}}{\text{Born}}_{\Gamma=0})/\alpha^{a \equiv \Delta}{\text{LO}} = \kappa^{{\text{LO}}_0 + \kappa}{\text{LO}}_1 \cdot \alpha + \mathcal{O}(\alpha^{2) $, the statement that difference is higher order is equivalent to state that $\kappa}{\text{LO}}_0=0$. At NLO, this relation translates to :

$((\mathcal{A}^{{\text{Virtual}}_{\text{CMS}}+\mathcal{A}}{\text{Born}}_{\text{CMS}})-(\mathcal{A}^{{\text{Virtual}}_{\Gamma=0}+\mathcal{A}}{\text{Born}}_{\Gamma=0}))/\alpha^{{a+1} \equiv \Delta}{\text{NLO}} = \kappa^{{\text{NLO}}_0 + \kappa}{\text{NLO}}_1 \cdot \alpha + \mathcal{O}(\alpha^{2) $}

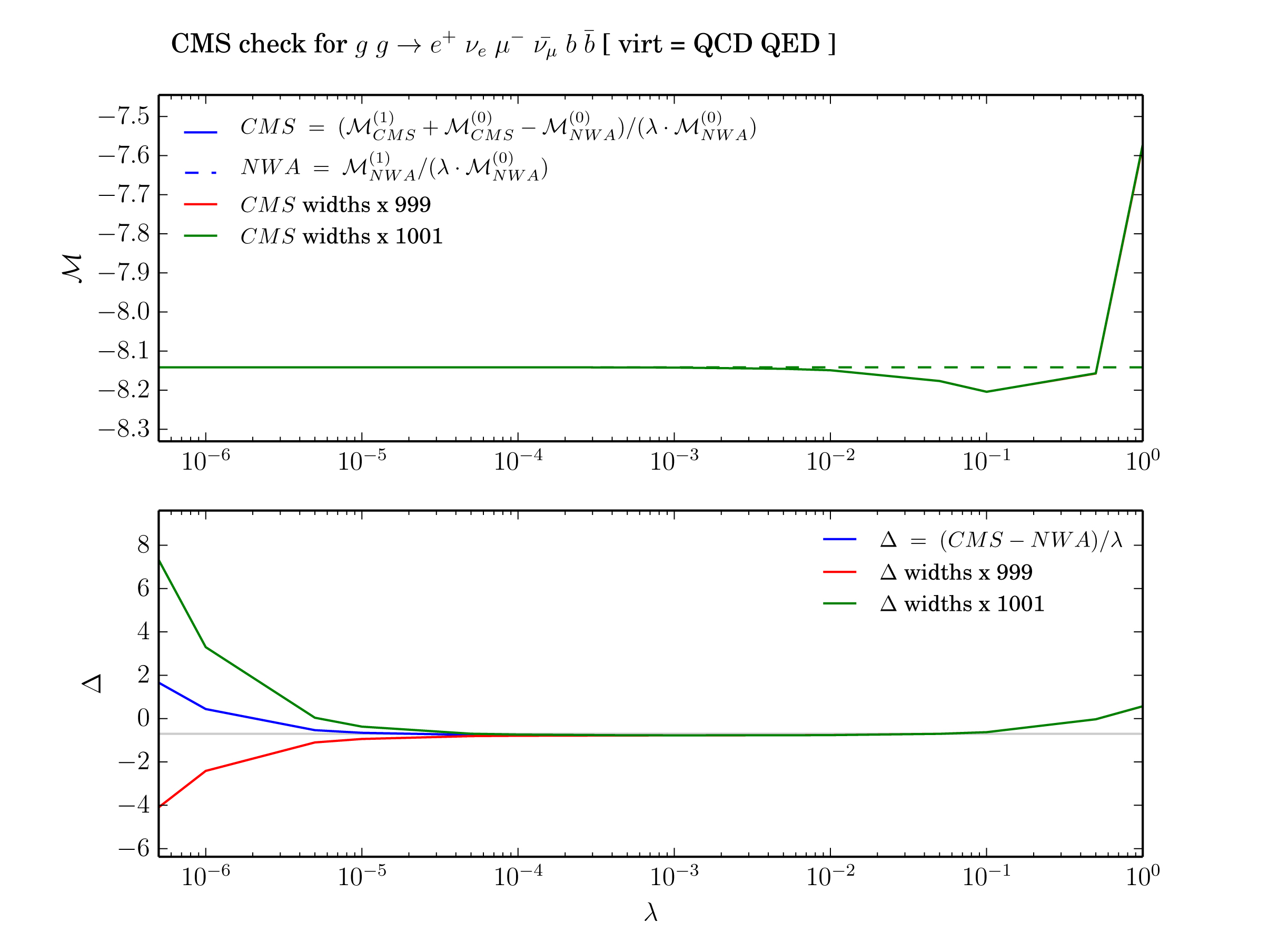
In order to check that $\kappa^{{\text{LO}}_0$ and $\kappa}{\text{NLO}}_0$ are indeed zero, the test proceeds by scaling down all relevant couplings and widths by the parameter $\lambda$ and to evaluate the expressions of $\Delta$ for many progressively smaller values of \lambda but always on the same offshell kinematic configuration. One can then plot the quantities $\Delta^{{\text{NLO|LO}}/\lambda$ and make sure that the asymptot for small values of lambda is the constant $\kappa}{\text{NLO|LO}}_1$. Any divergent behavior would be a manifestation of the presence of the term $\kappa^{{\text{NLO|LO}}_0/\lambda$ which reveals an issue with the CMS implementation (most likely one of the two points mentioned above) which spoils the expected cancellation. Before we detail the option of this test, here is the expected output (generated automatically, incl. this plot) for the case of QCD and QED corrections to fully decayed top quark pair production:}

In the upper inset, we clearly see the finite width effects for large values of $\lambda$. These become progressively smaller and indiscernible below $10^{{-3}$. When dividing this difference by lambda, as done in the lower inset, we only see a mild deviation with respect to a constant. Changing the LO width used for the test by as little as 0.1 % already yields a larger $\kappa}{\text{NLO}}_0$ than the residual one stemming from numerical inaccuracies. Changing the analytical continuation of the logarithms of the UV wavefunctions counterterms to make them incorrect would yield an asymptot in the $\Delta^{{NLO}/\lambda$ plot of the order of thousands, clearly assessing the sensitivity of the test towards any incorrect CMS implementation at NLO.}

We now focus on the description of the command, whose main syntax is

MG5_aMC> check cms [-reuse] <process_definition> <options>

Basic Syntax Rules

• Use a ">" to separate the initial state particle(s) from the final state ones.

• Initial state can be one (decay) or two (scattering) particles.

• Use " x x > z > y y y " form to require particle z to appear in a s-channel intermediate state (not recommended due to gauge invariance).

• Use " x x > y y y $ z" form to forbid particle z from appearing in a s-channel intermediate state (not recommended due to gauge invariance).

• Use " x x > y y y / z" form to exclude particle z to appear as internal particle in any diagram.

• Use comma to specify decay chains. For instance "x x > Z W, Z >y y, W > k k" means "x x > Z W" where Z then decays to yy and W to kk.
• Coupling orders are automatically detected to generate the leading order processes. To explicitly specify coupling orders, add them after the process on the same line:
  x x > y y y / z QCD=0
  x x > Z W QED=2, Z > y y, W > k k
  Note that if a coupling order is omitted, it defaults to infinity (or, for restricted couplings such as HIG in the HEFT model, to the restricted value).
• Use the multi-label "p" to indicate a proton or an anti-proton.
  The symbol "p~" does not exist. In fact the type of initial state (pp or ppbar or parton-parton fixed energy) is specified later, during the run, in the run_card.dat.
  The multi-lable "j" suggests a final-state jet.
• Note that the syntax for MadGraph 5 differs slightly from previous versions: a space (" ") is required between particle names, and the decay chain syntax has been upgraded to a more powerful syntax which allows better control of the different processes.

Process Examples

PROCESS

Sample Diagram

Notes