A Color Triplet Model

Corresponding Authors

• Elizabeth Drueke (Michigan State University)
• Reinhard Schwienhorst (Michigan State University)

Other Contributors

• Natascia Vignaroli (Michigan State University)
• Joseph Nutter (Michigan State University)
• Devin G. E. Walker (SLAC National Accelerator Laboratory)
• Jiang-Hao Yu (The University of Texas at Austin)
• Tao Han (University of Pittsburg)
• Ian Lewis (University of Wisconsin)
• Zhen Liu (University of Wisconsin)

Description of the Model

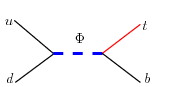
The color-triplet (Phi) is a heavy hadronic resonance with fractional electric charge. The Feynman diagram for decay to tb is below.

In particular, it is possible to produce triplet, anti-triplet, and sextet particles; but the LHC is a proton-proton machine and so the triplet production is enhanced by the parton-parton luminosity of the quark-quark initial state. The contributing quark-quark initial states are QQ, QU, QD, and UD, where Q, U, and D denote the SM quark doublet, up-type singlet, and down-type singlet, respectively. The diquark particles could be the spin-0 scalars with

$SU(3) \times SU(2)_L \times U(1)_Y$

quantum numbers

$\Phi \simeq (6 \oplus \overline{3}, 3, \frac13), \quad \Phi_U \simeq (6 \oplus \overline{3}, 1, \frac13),$

and the spin-1 vectors

$V^\mu_U \simeq  (6 \oplus \overline{3}, 2, \frac56), \quad V^\mu_D \simeq  (6 \oplus \overline{3}, 2, -\frac16).$

To produce the tb final state, the charge of the colored particle needs to be 1/3. The gauge-invariant Lagrangian can be written as:

$\mathcal{L}_{\rm diquark} = K^j_{ab} [\kappa_{\alpha\beta} \overline{Q^C_{\alpha a}}i\sigma_2 \Phi^{j} Q_{\beta b} + \lambda_{\alpha\beta} \Phi_U \overline{D^C_{\alpha a}}U_{\beta b} + \lambda^U_{\alpha\beta} \overline{Q^C_{\alpha a}}i\sigma_2\gamma_\mu{V^{j}_U}^\mu U_{\beta b} +$ 

$\lambda^D_{\alpha\beta} \overline{Q^{C}_{\alpha a}}i\sigma_2\gamma_\mu{V^{j}_D}^\mu D_{\beta b}] + \rm{h.c.}$

where

$\Phi^j = {1\over 2}\sigma_{k} \Phi_{k}^{j}$ 

with the

$SU(2)_{L}$ 

Pauli matrices

$\sigma_{k}$

and color factor

$K^j_{ab}$.

The couplings to QQ, and to U and D, are given, respectively, by

$\kappa_{\alpha\beta}$ \rm{ and } $\lambda_{\alpha\beta}$.

Here a, and b are quark color indices, and j is the diquark color index with

$j=1-N_D$,

where N_D is the dimension of the (N_D=3) antitriplet or (N_D=6) sextet representation. C denotes charge conjugation, and alpha and beta are the fermion generation indices. After electroweak symmetry breaking, all of the SM fermions are in the mass eigenstates. The relevant couplings of the colored diquark to the top quark and the bottom quark are then given by

$\mathcal{L}_{qqD} = K_{ab}^{j} \left[  \kappa^\prime_{\alpha\beta} \Phi \overline{u^c}_{\alpha a} P_\tau d_{\beta b} + \lambda^\prime_{\alpha\beta} V_{D}^{j\mu} \overline{u^c}_{\alpha a} \gamma_{\mu}P_\tau d_{\beta b} \right]+ \mathrm{h.c.},$

where

$P_\tau = \frac{1\pm \gamma_5}{2}$

are the chiral projection operators. Assuming that the flavor-changing neutral coupling is small, the third-generation couplings are

$\mathcal{L}_{\rm top} = K_{ab}^{j} \Phi \overline{t^c}_\alpha P_\tau b_\beta + 
K_{ab}^{j} V^\mu \overline{t^c}_\alpha \gamma_\mu P_\tau b_\beta + h.c.$

The decay width of the color~triplet to tb is given by

$\Gamma (\Phi \to t\,b ) = \frac{g_{\Phi}^2}{8\pi}(1-x_t^2)^2 + {\mathcal O}(x_f\times x_b) + {\mathcal O}(x_b^2) \;,$

where

$x_t=\frac{m_t}{m_\Phi}$ \rm{ and } $x_b=\frac{m_b}{m_\Phi}$

and the color triplet coupling to tb is given by

$g_{\Phi}$.

See more details in

• ​1409.7607v2
• ​1010.4309v2

Model Files

• proc_card​: for generation of 500 GeV triplet (place in Cards/)
• run_card​: for generation of 500 GeV triplet (place in Cards/)
• Width Macro​: macro to generate widths for triplet at different masses
• modcolorS_trip​: the model

Generation specifics

In ​1409.7607v2, the samples were generated with the color triplet mass as the scale, dsqrt_q2fact1, and dsqrt_q2fact2 in the run_card.dat file. These samples were also generated without MadGraph cuts as demonstrated in the run_card.dat for 500 GeV mass included above. The specific generations run were

p p > t b, t > b l+ vl @1
p p > t~ b~, t~ > b~ l- vl~ @2

The resonanceWidth macro can be run to determine the width of the color triplet resonance, which is the WSIX parameter input for the parameters.py file in the model directory.

To generate the settings for a specific color triplet mass, change the MSIX parameter to the mass of the particle in GeV and the WSIX parameter as described above in the parameters.py file of the model.