Testing the complex mass scheme implementation

The complex mass scheme is the modern way of handling finite width effects of unstable particles in perturbation theory. In a nutshell, it consists in redefining the mass of unstable particles as complex with an imaginary part proportional to its width. The denominator of unstable propagators remains identical, but contrary to the naive implementation of the width, the complex mass will also appear in the numerator of fermion propagators and in all couplings proportional to the unstable particle mass. In doing so, the Lagrangian is simply continued to complex masses and the final result remains gauge invariant. The Complex Mass Scheme (CMS henceforth) can be activated by simply typing the following command in the interactive shell:

MG5_aMC> set complex_mass_scheme True/False

The CMS implementation is rather straightforward at leading-order (LO) but it becomes more involved at next-to-leading-order (NLO) because of mainly two points

• The widths must be LO accurate at least in the offshell region and NLO accurate in the onshell region.
• The logarithms appearing in the UV wavefunction renormalization must be evaluated in the correct Riemann sheet.

The details of these issues will be discussed in a forthcoming publication; This wiki page is mainly to describe the various options to the command 'check cms' which automatically tests the consistency of the CMS implementation. The core idea of the test is to compare amplitudes in the CMS scheme ($\mathcal{A}_{\text{CMS}}$) and in the case of widths set to zero ($\mathcal{A}_{\Gamma=0}$) for a given kinematic configuration where all resonances are far off-shell. The difference between these two amplitudes must be higher order. More formally, this means $\mathcal{A}^{{\text{Born}}_{\text{CMS}}\sim \mathcal{A}}{\text{Born}}_{\Gamma=0} \sim \mathcal{O}(\alpha^a)$.

At LO, we can write $(\mathcal{A}^{{\text{Born}}_{\text{CMS}}-\mathcal{A}}{\text{Born}}_{\Gamma=0})/\alpha^{a \equiv \Delta}{\text{LO}} = \kappa^{{\text{LO}}_0 + \kappa}{\text{LO}}_1\alpha + \mathcal{O}(\alpha^{2) $. The statement that the difference is higher order is then equivalent to state that $\kappa}{\text{LO}}_0=0$.

At NLO, this relation becomes $((\mathcal{A}^{{\text{Virtual}}_{\text{CMS}}+\mathcal{A}}{\text{Born}}_{\text{CMS}})-(\mathcal{A}^{{\text{Virtual}}_{\Gamma=0}+\mathcal{A}}{\text{Born}}_{\Gamma=0}))/\alpha^{{a+1} \equiv \Delta}{\text{NLO}} = \kappa^{{\text{NLO}}_0 + \kappa}{\text{NLO}}_1\alpha + \mathcal{O}(\alpha^{2) $}

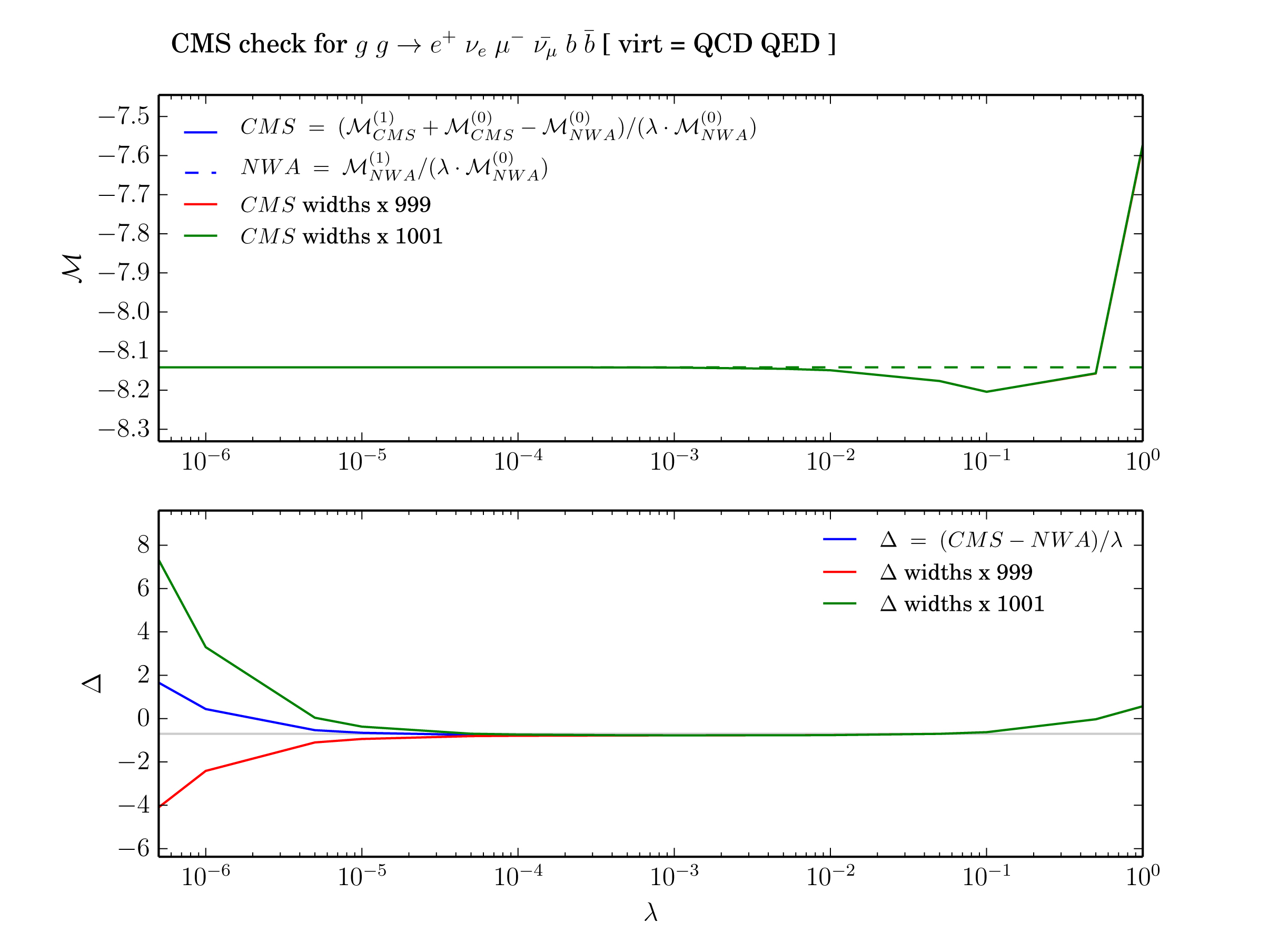
In order to check that $\kappa^{{\text{LO}}_0$ and $\kappa}{\text{NLO}}_0$ are indeed zero, the test proceeds by scaling down all relevant couplings and widths by the parameter $\lambda$ and to evaluate the expressions of $\Delta$ for many progressively smaller values of \lambda but always on the same offshell kinematic configuration. One can then plot the quantities $\Delta^{{\text{NLO|LO}}/\lambda$ and make sure that the asymptot for small values of lambda is the constant $\kappa}{\text{NLO|LO}}_1$. Any divergent behavior would be a manifestation of the presence of the term $\kappa^{{\text{NLO|LO}}_0/\lambda$ which reveals an issue with the CMS implementation (most likely one of the two points mentioned above) which spoils the expected cancellation. Before we detail the option of this test, here is the expected output (generated automatically, incl. this plot) for the case of QCD and QED corrections to fully decayed top quark pair production:}

In the upper inset, we clearly see the finite width effects for large values of $\lambda$. These become progressively smaller and indiscernible below $10^{{-3}$. When dividing this difference by lambda, as done in the lower inset, we only see a mild deviation with respect to a constant. Changing the LO width used for the test by as little as 0.1 % already yields a larger $\kappa}{\text{NLO}}_0$ than the residual one stemming from numerical inaccuracies. The figure on the left shows that incorrectly setting the analytical continuation of UV wavefunctions counterterms logarithms yields an asymptotic value of several thousands in the $\Delta^{{NLO}/\lambda$ plot. This clearly establishes the sensitivity of the test towards any incorrect CMS implementation at NLO.}

We now focus on the description of the command for this check, whose main syntax is

MG5_aMC> check cms [-reuse] <process_definition> <options>

• Ex.: check cms -reuse u d~ > e+ ve a [virt=QCD QED] --name=udx_epvea --tweak=['default','allwidths->allwidths*0.99(widths_x_0.99)']

First, the '-reuse' suffix following 'cms' specifies that you want to reuse relevant information existing from previous runs. This includes potentially reusing the fortran output of the NLO matrix element if the same process was run before with the 'cms check' command. Also, if a name was given to this run (see option '--name' further) and the corresponding saved result python pickled file exists on disk, this run will be skipped and the result recycled from the pickle file. When '-reuse' is not specified, the test always restarts from scratch. In general, it is recommended to always use '-reuse'.

The <process_definition> which follows can be any process following the MG5 syntax. If this process is LO, the test will be adapted to test $\kappa^{{\text{LO}}_0$ and the matrix element will be generated an evaluated dynamically directly in python. If the process definition is at NLO, then the test will test $\kappa}{\text{NLO}}_0$ and the output will be done in fortran on disk, compiled and the corresponding standalone 'check' executable steered by MG5_aMC. The LO CMS test is mostly trivial, but it can be useful to investigate the expected sensitivity on the CMS implementation of the corresponding NLO process.

Finally, the following options are available and we detail their usage in the next sections.

• Basic options
  • --name
  • --tweak
  • --seed
  • --offshellness
  • --energy
  • --lambdaCMS
  • --show_plot
  • --recompute_width
  • --CTModeRun
  • --helicity
  • --reduction
• More technical options
  • --cms
  • --diff_lambda_power
  • --loop_filter
  • --resonances
• Special option
  • --analyze

Basic options

--name=auto

This will serve as the base_name for the fortran output folder for the loop matrix element and for the pickle files storing the results generated. The default 'auto' tries to smartly automatically assign one, but it is recommended to specify your own.

• Example: --name=fully_decayed_ttx

--tweak=default()

The tweak option is an important one as it lets you automatically performs changes to the computational setup which should deteriorate the quality of the CMS check (i.e. induce non-zero values of $\kappa^{{\text{NLO}}_0$) so that one can appreciate to which level of accuracy the current implementation is consistent. The keyword 'default' means no changes and would yield the blue curve in the figures below. What follows the tweak in parenthesis is its name which will be used to label the curve and to build the name of the pickle file storing this tweak. Possible tweak ares:}

• <param_name>->expr(<param_name>): for instance 'WZ->1.1*WZ' would multiply the LO-accurate Z-boson width by 10%. Notice that you can use the keyword 'allwidths' which will automatically apply the rule to all widths.
• seed<int>: for instance seed669 which specifies that for this tweak one must change the seed to value <int>
• [logp|logm|log]->[logp|logm|log]: for instance logp->logm which would change the matrix element fortran output so as to change the logarithms continued with '+2$\pi$i' to '-2$\pi$i'

These tweaks can be chained together with the symbol '&' to form a bigger tweak, e.g. '--tweak=WZ->1.01*WZ&logp->logm&logm->logp(Widths_changed_and_log_inverted)' which runs the CMS test with both the logs inverted and the width changed. Finally, one can put these global tweak in a list (with string quotes) to have MG5_aMC run them one after the other (if their pickle file is not found and recycled) and plot together.

• Example: --tweak=['default','allwidths->1.1*all_withds&seed333(Increased_widths_and_seed_333)','logp->logm&logm->logp(inverted_logs)']

In this case one will make the CMS test successively in three different setups. The first one is the original one (where it is supposed to pass). The second one is for a different kinematic configuration and all widths increased by 10%. Finally the last one inverts the analytic continuation of all logs.

• Example: --tweak=alltweaks

This is a shorthand for the specification of all tweaks typically relevant; that is --tweak=['default','seed667(seed667)','seed668(seed668)','allwidths->0.9*allwidths(widths_x_0.9)','allwidths->0.99*allwidths(widths_x_0.99)','allwidths->1.01*allwidths(widths_x_1.01)','allwidths->1.1*allwidths(widths_x_1.1)','logp->logm(logp2logm)','logm->logp(logm2logp)']

--seed=666

Changes the seed for the generation of the offshell kinematic configuration, allowing for varying the config. The value '-1' sets it so that it is different for every run.

• Example: --seed=667

--offshellness=10.0

Sets what is the minimum requirement of offshellness for each resonance that the kinematic configuration must satisfay. The default offshellness $\chi$ of 10 is such that the momentum of each resonance must satisfy $p^{2>(\chi+1)M$. The offshellness can be negative too, but always strictly larger than -1. Notice that when the offshellness required is negative, it is not guaranteed that MG5_aMC will find a valid kinematic configuration if external states are massive. Finally, notice that the phase kinematic configuration chosen satisfies extra requirement of isolations and hardness in terms of a minimal pt cut and $\delta$R between all external legs.}

• Example: --offshellness=-0.7

--energy=5000.0

Sets the target energy for the kinematic configuration to build. Notice that this energy will be automatically changed with a warning depending on its consistency with the offshellness required.

• Example: --energy=2000.0

--lambdaCMS=(1.0e-6,5)

Sets what values of the scaling parameter $\lambda$ must be used for the test. This option can either be a tuple '(min_val, points_per_decade)', a float 'min_val' or a python list. The float 'min_val' is the minimal value of $\lambda$ to probe and $points_per_decade$ is the number points one should spread uniformly in each decade (i.e. interval [$10^{-i+1},10-i$]. Notice that the list must always contain the value 1.

• Example: --lambdaCMS=(1.0e-2,5)

With this option, the list of $\lambda$ values used will be: [1, 0.8, 0.6, 0.4, 0.2, 0.1, 0.08, 0.06, 0.04, 0.02, 0.01]

• Example: --lambdaCMS=[float('1.0e-%d'%exp)\ for\ exp\ in\ range(8)]

With this option, the list will be evaluated and the return list will be used, i.e.: [1.0, 0.1, 0.01, 0.001, 0.0001, 1e-05, 1e-06, 1e-07]. Notice that spaces must be escaped and this options should be placed last for parsing reasons.

--show_plot=True

Allow to turn off the matplotlib generation and only report the outcome of the numerical check. Turning it off also removes the progress_bar display during the check

• Example: --show_plot=False

--recompute_width=auto

Decides how to compute the leading-order accurate width necessary for the test to pass. Four possible values 'never', 'first_time', 'always' or 'auto'. 'never' means that the width for $\lambda=1$ will be taken from the value in the default param_card .dat and the widths for subsequent smaller values of $\lambda$ will be computed via a simple scaling law. 'first_time' means that the widths will be computed (numerically or analytically if the model has a decay module) with MadWidth' for $\lambda=1$ and scaled down for lower $\lambda$ values. 'always' means that the widths will be recomputed for all $\lambda$ values (this mode is only to be used for checking the width computation). Finally the default value 'auto' will be interpreted as 'never' for an LO test where LO-accurate width aren't necessary in the offshell region and 'first_time' if the check is NLO.

• Example: --recompute_width=never

--CTModeRun=-1

By default MadLoop will run in double precision, make stability tests and only if they are unsuccessful go to quadruple precision. Given the nature of the cancellation we are probing with this test, the $\Delta/\lambda$ plot can quickly become unstable for complicated processes and low $\lambda$ values. It is then necessary to force MadLoop to perform the test in quadruple precision. This can be done by changing this option from its default -1 (which is where it performs stability tests) to 4 (forced quadruple precision).

• Example: --CTModeRun=4

--helicity=-1

The default value of -1 means that the test is performed with the matrix element summed over all helicity configurations. This can be slow when enforcing quadruple precision and looking at complicated processes. With this parameter set to '--helicity=<int>', the matrix elements will be evaluated on only the helicity configuration #<int> (check their order in the file HelConfigs.dat of the directory MadLoop5Resources output along with the process).

• Example: --helicity=1

--reduction=1|2|3|4

Specifies which reduction method to use and in which order (see comments on the option #MLReductionLib of the card MadLoopParams.dat for details.)

• Example: --reduction=3|1

This examples tell MadLoop to first try reducing with IREGI and then CutTools if unstable, but never use PJFry or Golem95.

More technical options

--cms=QED&QCD,aewm1->10.0/lambdaCMS&as->0.1*lambdaCMS

This is one of the most complicated options and it contains two parts separated by a comma. The first part lists the coupling orders which take part in the expansion. The second part lists how to scale the corresponding parameter which drive the expansion. These must be external parameters present in the param_card. The value 'lambdaCMS' is a special tag which refers to the current value of the scaling parameter $\lambda$ being considered. Notice that these replacement rules must be of the form <ext_param_name>->f(<ext_param_name>,lambdaCMS) where f is some function following python syntax. The default value start from fixed values 10.0 and 0.1 for $\lambda=1$, but it is possible to specify the original value of the parameter in the card like this 'aewm1->aewm1/lambdaCMS' in which case the base value of the external parameter aewm1 will be the one in the original param_card.dat. You should not need to change this default unless you are testing a new physics model with an extended gauge sector (in which case the modification could look like the example below).

• Example: --cms=QED&QCD&NP,aewm1->10.0/lambdaCMS&as->0.1*lambdaCMS&newExpansionParameter->newExpansionParameter*lambdaCMS

--diff_lambda_power=1

This controls by which power to divide the difference term $\Lambda$. The default is of course equal to one so as to test $\kappa^{{\text{NLO|LO}}_0=0$ but at LO it is sometimes interesting to divide $\Delta$ by $\lambda}2$ so a to see if $\kappa^{{\text{LO}}_1$ is vanishing as well. This is expected to be the case for all $2\rightarrow2$ processes (i.e. the plot of $\Delta/\lambda}2$ has a constant asymptot as well, so that $\kappa^{{\text{LO}}_1=0$). For such processes, the higher order contribution $\kappa}{\text{NLO}}_0$ is zero by construction and the test is not sensitive to the CMS implementation

• Example: check cms u d~ > e+ ve --diff_lambda_power=2

--loop_filter=None

Allows to specify a conditional expression to impose a requirement on the loop diagrams to be kept. This expression can only be an pyton expression of involving the following variables : 'n', the number of loop propagators; 'id' the loop diagram number as it can be read in the postscript generated with the command display diagrams; 'loop_pdgs' the list of absolute values of the PDG of the particles running in the loop; 'loop_masses' and 'struct_masses' the list of the parameter names of the masses running in the loop and the masses of the particles directly attached to the loop.

• Example: --loop_filter='n>3'

Selects only box diagrams and above.

• Example: --loop_filter='n<4 and 6 in loop_pdgs and 3<=id<=7'

Selects only triangle loop or smaller, with at least a top running in the loop and whose ID is in the range [3,7].

--resonances=1

Several kinematic configurations are constructed starting from each of the resonances detected in the process. Given that all resonances are anyway offshell, it is only necessary to run the test on one of these particular kinematic configurations. This option let you chose to instead run the test on the first 'n' such kinematic configurations. Alternatively, one can also specify the resonance(s) one wishes to run on, by specifying tuples '(resonance_PDG,(resonance_mother_numbers))'. Keep in mind however that no matter which kinematic configuration is picked, *all* resonances are tested at the same time, so this option is a bit superfluous as it is completely similar as only changing the seed.

• Example: --resonances=3

Run on the kinematic configurations generated starting from the first three resonances founds.

• Example: --resonances=(24,(3,4))

Run on the kinematic configuration generated starting from a W decaying into particles with leg number 3 and 4.

• Example: --resonances=[(24,(3,4)),(24,(4,5))]

Run on the kinematic configurations generated starting from a W and a Z (decaying into particles 3,4 and 4,5 respectively).

Special option

--analyze=None

This option must be used without any process definition. It is intended to specify the path of pickle files storing the results of previous results to be re-analyzed and replotted. A common usage of this option is:

• Example: check cms --analyze=my_default_run.pkl,increased_widths.pkl(Increased_widths),logs_modified.pkl(Inverted_logs),seed_668.pkl(Different_seed)

This will reanalyze the data in my_default_run.pkl and plot them while also including the curves from the list of pickle paths following the first one. The name in parenthesis will serve as the legend (underscores will be replaced by spaces)