|
|
News:
[10/05/2016]:
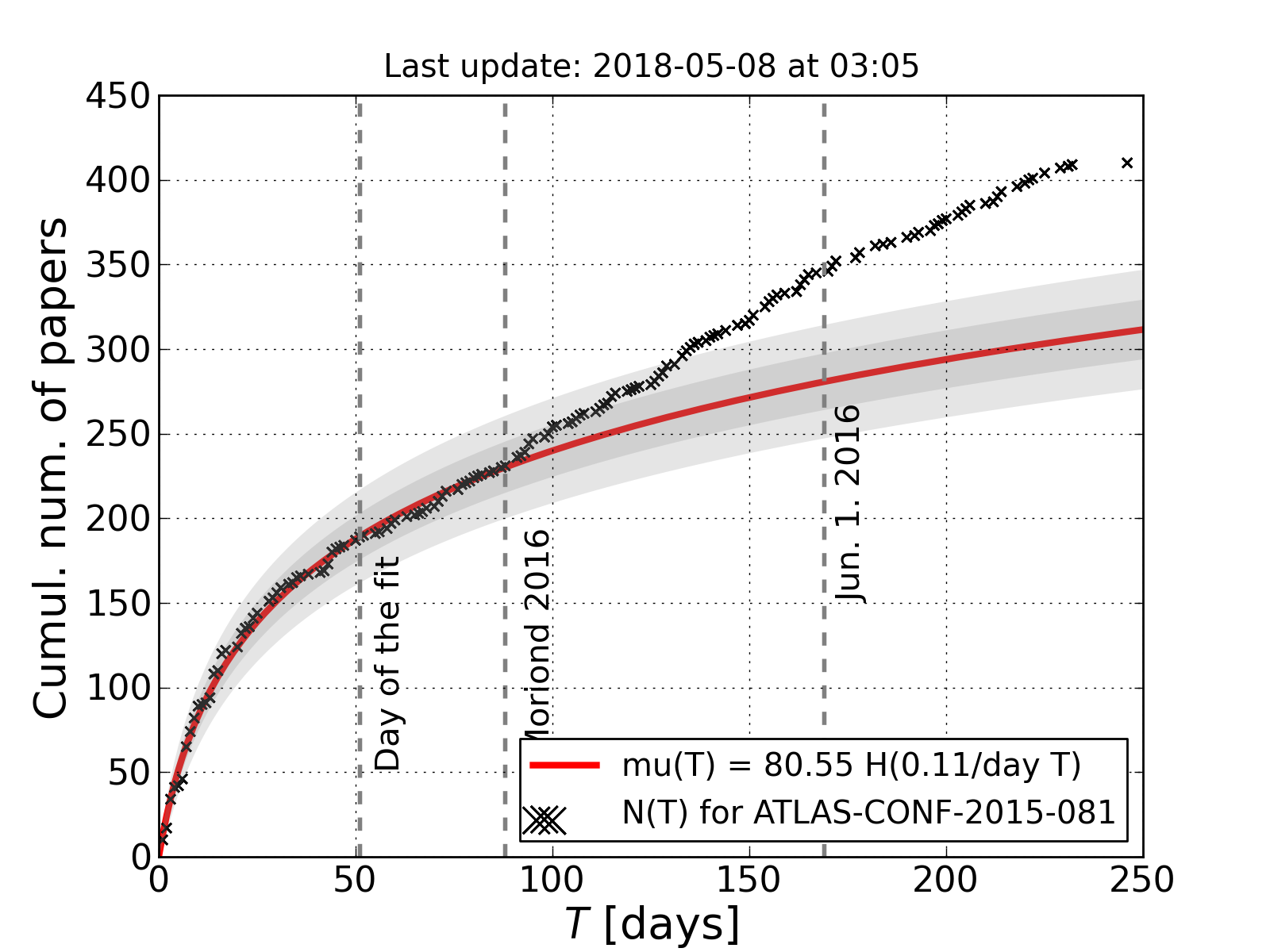
The fit resulting from
the first 50 days of
data is failing.
Information introduced
at Moriond 2016
clearly resulted in
the cutoff for the
validity of the theory
(the first plot with
the red curve shows
this nicely). The fit
had a nice run though.
Data was within 2
sigma of the
prediction for about
130 days (almost three
months after the fit)!
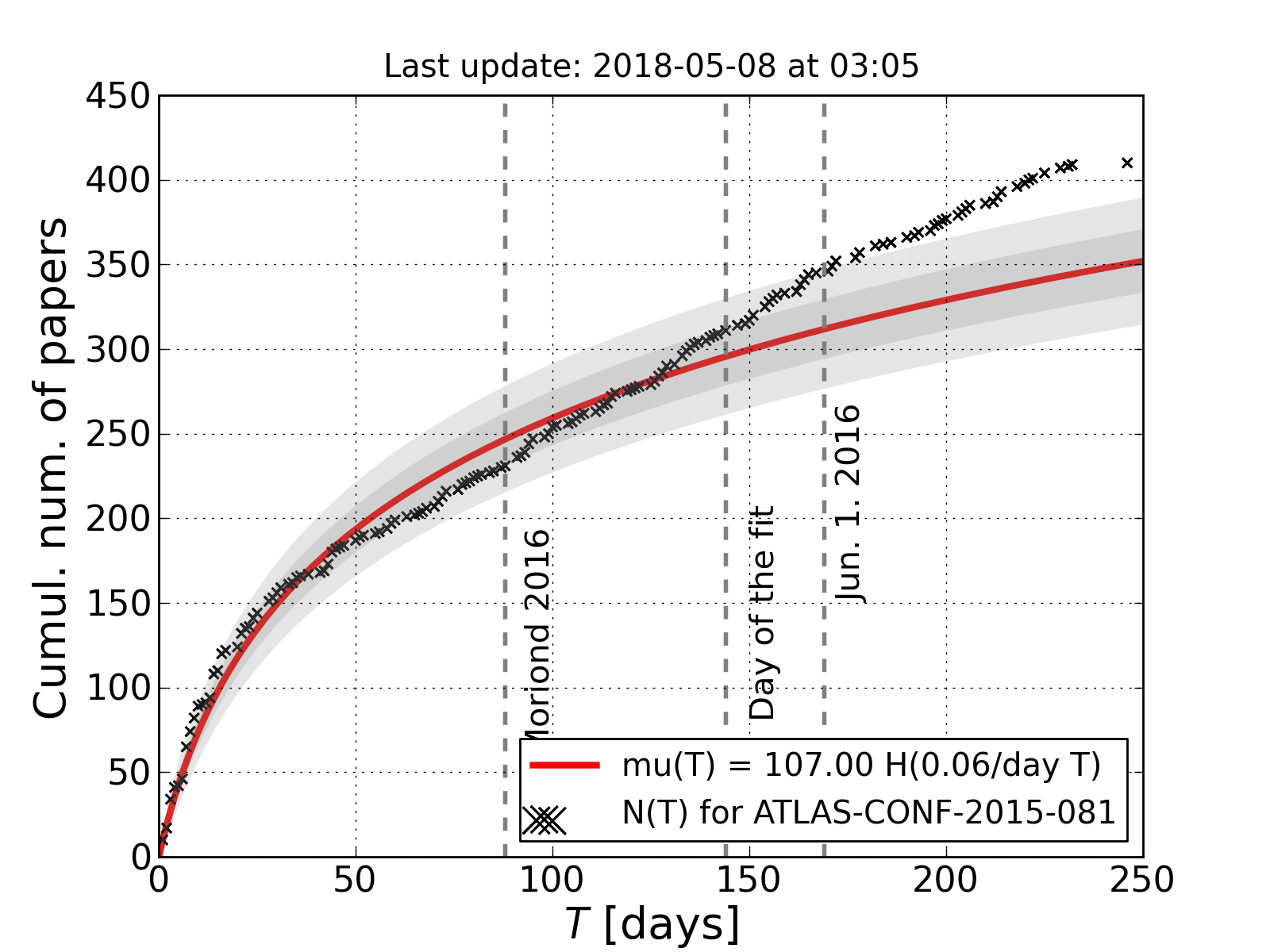
The functional form
still holds. I added a
plot using all the
data to date for fun
(second plot with a
red curve).
[17/03/2016]:
We got a new submission! See
below for more details!
[17/03/2016]:
The original fit using the
first 50 days of the data
has been modified to include
papers which retroactively
cited the ATLAS di-photon
result, and are included in
the current data set. Big
thanks to Bradley
Kavanagh for super
useful discussions about
the data!
|
The
goal of the game is simple:
Can you
predict the number of papers on
the di-photon resonance on Jun.
1. 2016?
The
rules:
1.
You can use only the first 50
days of data to make the
prediction.
2.
The model has to have 2 or
less fit parameters.
Notes:
You can download the
current data set from the link
on the left side.
The data is formatted as
following:
<Date> <Days
from beginning> <Num. of
papers on date> <Total
num. of papers>
Data N(T) represents
the number of citations to
ATLAS-CONF-2015-081 as a function of
time. Papers which appeared before
Dec. 15h 2015 and cite the note
retroactively, as well as papers which
do not have an arXiv code, are
excluded.
The citation data is extracted from
the inSPIREs website and can hence
lag compared to the information on
arXiv.
The starting day is marked as 1,
measured from Dec. 15th 2015.
Send
your submissions to mbackovic
.at. gmail
See the current predictions below...
|
|
|
15/12/2015:
ATLAS/CMS di-photon
resonance
model info:
Poisson distribution with a
two parameter Harmonic
number (di-gamma function)
as the mean. Least-squares
fit.
by: Mihailo
Backović.
|
|
15/12/2015:
ATLAS/CMS di-photon
resonance
model info:
1 parameter fit! The model
assumes that the number of
papers per day is constant
over the course of a week, but
that the number of papers per
week decays like 1/t.
by: Bradley Kavanagh
|
|
All
the data and information on
this website is public and can
not be used for ANY commercial
purposes!
|
|
|
|
|